Author: Andrés Rieznik
Senior Researcher
@AndresRieznik
Optimizing the cost of behavioral experiments on hackers' motivation

Our cost-aware algorithm converges much faster towards the true generating model, at a much faster rate per unit cost, than a random or a conventional ADO strategy.
One of the main goals we have in the BitTrap Attacker Behavioral Labs is to know the answer to a single question: once an attacker was successful in trespassing a system and when the hacker is interested in monetizing his hack, would he rather secure a bounty from his victims in exchange for revealing the hack rather than continue looking for a potential reward? What would be the minimum amount he would accept?
Bittrap service places Bitcoin wallets including an unspent transaction and the credentials required to spend the transaction in different places of a system. A hacker who has compromised a BitTrap-protected asset, who furthermore is aware of the wallet, may decide to spend the transaction. Collecting this (bounty) triggers an incident-response operation that alerts the organization of the breach, effectively causing the hacker to reveal his presence. Then, the vulnerability can be immediately assessed and patched while avoiding ransomware and data exfiltration altogether. But… will he collect the bounty? And the follow-up question: under what circumstances will he collect it?
Of course, if the amount placed in the wallet is very high, let's say orders of magnitude higher than what the hacker expects to gain with the attack, he will be enticed to accept. But in this case our strategy would not make sense, it may be less costly to be attacked. Ideally, the amount of bitcoins placed in the wallet needs to be enough to entice the hacker to accept, but not much higher.
This amount can be estimated empirically. Given that each hacker behaves differently, this estimation is also statistical. There is a probabilistic distribution that drawing a random hacker answers what is the minimum amount he is willing to accept. For example, one may collect public information about ransomware attacks, including what are the amounts asked and paid, in order to determine an effective value. Say, by picking the 90th percentile, this would mean that 9 out of 10 hackers are comfortable with this value. Of course, when setting rewards for a subset of systems, say endpoints (e.g., desktops in a financial institution), the sampled ransomware attacks may be filtered to include only incidents for endpoints of the same subset.
Other than the publicly-available information, in the Bittrap Lab we conduct experiments using vulnerable and Bittrap-protected endpoints in the cloud with different reward values. Again, this information may be used to compute a reward value, e.g., the 90th percentile of the rewards cashed in the experiment. The full process consists in deploying these endpoints with different reward values, these values controlled by an AI algorithm we implemented that takes into consideration prior results and chooses the candidate reward with higher informative value per unit cost to continue.
How does our AI work? Running behavioral experiments is a costly process and requires careful design in order to test hypotheses while maximizing statistical power. In contrast to the canonical design in experimental economics and decision research, where a fixed set of experimental questions or offers are asked to all subjects or respondents, Adaptive Design Optimization (ADO) dynamically proposes choosing questions that maximize information gain considering previous answers [Yang, 2020; Chang, 2021]. Moreover, carefully selecting questions can minimize the number of times these questions are asked to obtain a given information gain and, if different questions have different associated costs, this fact can be included in the algorithms in order to minimize the cost of the experiment instead of the number of times a question is asked.
Different ADO versions have been developed in the behavioral science since the early 1990s (see [Ryan, 2016] for a review) but its adoption have been slow, in part because of the nontrivial technical skills required to implement them and, in part, because of its limitations. Limitations are due to the existing algorithms being so time-consuming that they are only practical in a few settings where the goal is to infer a behavior among a limited set of models. For instance, in memory research, the algorithm only works if the probability of remembering decays exponentially with time.
In particular, surprisingly as it may seem, in criminology there is a lack of rigorous experimental research (see e.g., [Dezember, 2020] and [Payne, 2020]). In fact, we are the first research team to implement an ADO approach to study hackers’ behavior. Moreover, we improved the existing algorithms so dramatically in terms of simulation speed that our method can be applied to infer hackers’ behavior without restricting to a set of pre-existing models, i.e., independently of how the probability of collection increases with the offered bounty. In each iteration, our algorithm selects the reward value we need to offer an intruder in order to maximize the expected information gain on hackers’ general behavior per unit cost, and obtains as a result the probability of each model.
A more detailed explanation of how our algorithm works can be found here: A new method to dynamically choose questions and minimize costs in behavioral experiments. In this article, we demonstrate its efficiency through “Ground truth” simulations: we create artificial data based on known models of hackers’ behavior and then apply this algorithm, and show how accurately and quickly the models can be recovered. Furthermore, we explain how our method is able to efficiently recover any monotonic function at any desired target accuracy, suggesting a huge range of applicability. Our results are currently under review in a scientific journal of high impact factor.
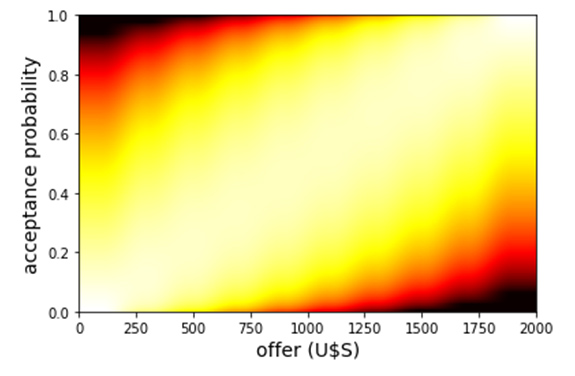
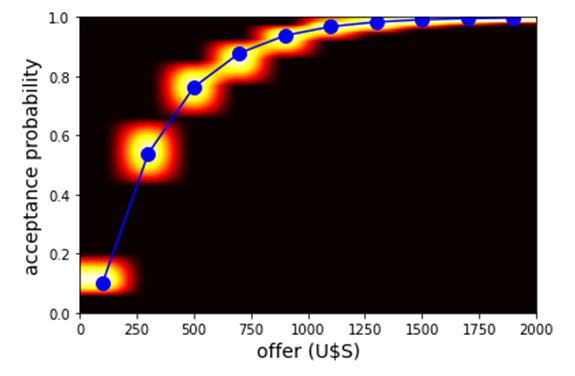
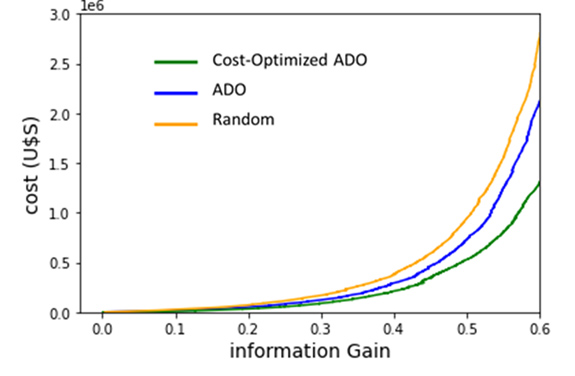
Below we show some evidence on how the algorithm works on artificially-prepared data. In Figure 1 we show the results of ground truth simulations assuming hackers behavior is given by the blue dotted line in the center plot. At the left we show a heat map representing our prior beliefs for this example regarding the probability of acceptance for rewards of different amounts. At the right, we show cost versus information gain for different algorithms. The center figure is a heat map plotting probability a hacker accepts versus reward amount that results after using our algorithm and obtaining an information gain of 60% relative to our priors. It is clear that our cost-aware algorithm converges much faster towards the true generating model, at a much faster rate per unit cost, than a random or a conventional ADO strategy.
a
b
c
a: Heat map representing our prior beliefs for the probability of acceptance as a function of the offered money.
b: Heat map (background) and true generating data curve (dotted blue) when the uncertainty is halved, i.e., when the information gained equals 50% of the initial uncertainty..
c: Information gain vs. cost using, using the prior shown in Figure 1a and the ground truth shown in blue in Figure 1b, for three different strategies: a conventional ADO strategy, a cost-aware ADO, and choosing randomly among the different offered amounts.
Using these methods we are systematically improving the effectiveness of our technology and learning about the characteristics of the different adversarial subpopulations. In each case we are able to optimally infer the bounty to be offered, maximizing the probability that an intruder will accept the offer and reveal his position.
References
Chang, J., Kim, J., Zhang, B. T., Pitt, M. A., & Myung, J. I. (2021). Data-driven experimental design and model development using Gaussian process with active learning. Cognitive Psychology, 125, 101360.
Dezember, A., Stoltz, M., Marmolejo, L., Kanewske, L. C., Feingold, K. D., Wire, S., ... & Maupin, C. (2020). The lack of experimental research in criminology—evidence from Criminology and Justice Quarterly. Journal of Experimental Criminology, 1-36.
Payne, B. K., & Hadzhidimova, L. (2020). Disciplinary and Interdisciplinary Trends in Cybercrime Research: An Examination. International Journal of Cyber Criminology, 14(1).
Ryan, E. G., Drovandi, C. C., McGree, J. M., & Pettitt, A. N. (2016). A review of modern computational algorithms for Bayesian optimal design. International Statistical Review, 84(1), 128-154.
Yang, J., Pitt, M. A., Ahn, W. Y., & Myung, J. I. (2021). ADOpy: a python package for adaptive design optimization. Behavior Research Methods, 53(2), 874-897.

